Vanilla Policy Gradient In JAX
A simple implementation using Acme
For this blog post, We’ll not only get into a Vanilla Policy Gradient (VPG) implementation, but perhaps more interestingly, do it in JAX. Note this post focuses on implementation; the theory of VPG is broken down in this post. Feel free to take a look at that first if you find yourself asking “why?”
We’re going to implement it piece by piece. The full code can be found at this repo.
The first line

Initialize networks
Warning: this section makes up the first half of this post. If you don’t feel you need to learn how to implement neural networks for RL in JAX, feel free to skip this section and head directly to the rest of the reinforcement learning loop.
We need a policy and a value function. Both will be represented by neural networks. I have found that for most starter Gym environments, two layers with 128 weights each do the job just fine (and often even less than this is needed).
The below code is adapted from the Acme implementation of PPO. Kudos to DeepMind for providing excellent baseline implementations of many RL algorithms.
Before we get started, let’s define some convenience classes which will allow us to organize our neural network and the functions related to it. This will also serve to give us a roadmap for building and initializing our neural networks.
This is pretty straightforward: for RL we need a network, a way to sample from the outputs of that network, and a way to compute the log probabilities of those samples (i.e., the actions). If you read that and didn’t think “yes, very straightforward,” consider reading the previous post.
sample() will take in the network output (i.e., info encoding the probability distribution) and a random number key, and return a sampled action.
log_prob() will take in the network output (again, the probability distribution) and an action, and return the log probability of that action.
In general our action will be a vector of real numbers (sometimes ints for discrete spaces), and our network will operate on batches of these.
Notice above that network is of type FeedForwardNetwork. Let’s take a look at the FeedForwardNetwork class. This is, again, a skeleton for us to fill out, and also a roadmap.
So, we need a way to initialize and apply our neural network, and for JAX, we need to ensure these are pure functions. Luckily, the haiku library takes care of most of the heavy lifting here, as we’ll see. For clarity, I’ve swept some type checking under the rug.
Let’s get cracking on the network!
Our VPG pseudocode specifies to initialize networks. The following MLP and Linear functions allow starting with various well-known initializations, falling under variance scaling. For this post we’ll just use the defaults without specifying those arguments.
Starting with the value function:
Why haiku?
By the way, you may be wondering “why haiku instead of flax?” Well, the immediate reason is that personally, I’m more used to it. They’re very similar, application-wise, so you should just stick with what works for you.
Highly subjective opinion warning: the feeling I get is that the collection of the Deepmind repositories are less the result of a “wild-west, every small team publishing for themself” environment. Rather, the collection of repos has a sense of cohesion and coordination. I could be wrong about this. Anyway, Deepmind has done a good job open sourcing a ton of their software stack related to reinforcement learning and deep learning, not limited to haiku. Check it out!
Now, we almost have an MLP which can serve as our value function, with a single output: the value given the observation! However we’re missing two things: proper input and output dimensions.
We need to tell the model what input dimensions (from the batch of observations) we expect. We’ll leave this as a dummy obs variable for now - we’ll come back to it in a minute. We would like to flatten the input, except for the batch dimension. That is, for batch size n, we want n observation vectors. We define the following function to do so:
…and prepend a call to this function to our code like so:
More than one batch dimension in JAX?
We assume the observation above has one batch dimension (e.g., 64, 128, etc. This is the batch size.). However, if you’ve gone poking around in other JAX examples online, you may notice an extra dimension out front in the main training loop. This is typically the device dimension.
Suppose typically I have a set of dimensions that looks like (batch_size, obs_size), like (128, 64). Adding a device dimension would look like (num_devices, batch_size, obs_size). Across one device, this would look like (1, 128, 64). However, parallelizing across two devices, this would look like (2, 64, 64). Our total batch size remains unchanged, but you can see the batch has been split across the two devices.
Our inner functions (like the past few code blocks) which take in obs don’t see the device dimension; from their perspective it doesn’t exist, so you can write these as if you only had one device. pmap() takes care of mapping the full computation to devices, though I won’t cover its usage here; see the documentation. As you can see in those examples, it’s only in the main training loop you need to worry about adding a device dimension to your tensors.
Finally, we’d like to make sure the output of our value function is a batch-sized vector of values if it isn’t already, so we squeeze the output results. Putting all of this into a haiku Sequential model yields:
This completes our value network!
Now, our policy model is slightly different.
First, because we are assuming a continuous action space, we need to output a distribution over actions, from which the actual action for some observation will be sampled. The policy model will output mean and variance to describe this multivariate normal distribution. Two fully connected layers are branched from the torso, to be able to learn mean and variance from the same embedding of the observation. For this reason, we don’t use hk.Sequential.
Here is the torso:
Now we add a branch each for the mean and variance.
Constrain to a positive scale, as variance must be positive.
Why softplus?
ReLU will compute faster, and may be a choice worth considering if compute power/training speed is a concern. However, if the user has problems with ReLU “dying” in the zero region (when \(x < 0\), \(y = 0\)), we cannot use leaky ReLU, the usual first solution to this problem, because the output must be positive. Softplus is a better option in this case.
We’re not quite done just yet, because of the vagaries of JAX. We need to wrap and transform the models we’ve just written.
First, we encapsulate our policy code into a function:
Then, we wrap both the policy and value functions into one forward function, outputting everything we infer from the observation from this function.
Finally, we use the haiku transform() function.
An aside on transform(), JAX, and pure functions
If you don’t care about why we use transform, so much as that it makes deep learning fast, feel free to skip this section.
From the haiku documentation:
…Haiku modules are Python objects that hold references to their own parameters, other modules, and methods that apply functions on user inputs. On the other hand, since JAX operates on pure function transformations, Haiku modules cannot be instantiated verbatim. Rather, the modules need to be wrapped into pure function transformations.
Haiku provides a simple function transformation, hk.transform, that turns functions that use these object-oriented, functionally “impure” modules into pure functions that can be used with JAX.
See here for pure functions, and here for why pure functions are required.
In short, JAX uses cached compilations of functions to speed everything up.
As you, a computer scientist, probably know, an optimizing compiler (here, XLA) converts your code into a form that is both lower level (closer to machine instructions), and able to make certain assumptions to run your computations in fewer steps. Oh yeah, compilation is great!
But of course, anyone who’s written anything moderately sized in C/C++ knows that repeated compilation will send your productivity straight in the trash, right next to the greasy pizza boxes and used Kleenex, never to be seen again. Can we avoid unnecessary compilation?
By mandating pure functions, JAX knows the function’s behavior is only dependent on its inputs, and so not only will it never need to be recompiled after the first time it’s used. Tt will be able to make more assumptions to improve its computational efficiency all the more so!
So, without further ado, let’s transform our model!
Now that we’ve transformed (“purified/JAX-ified”) our model, we’ve exposed a pure interface to our model we can use without worry: that is, forward.init(), and forward.apply().
We’ve additionally wrapped this with hk.without_apply_rng(). Our forward function’s apply method may require randomness in general, e.g. if it uses dropout layers during training. In our case, an rng key is not required, so we use this convenience wrapper to avoid needing to pass in an extra parameter when calling apply().
Let’s initialize our model by creating a dummy observation with the same dimensions as the real inputs to the model, and passing this to init(). The model will then be configured to handle the correct input and batch dimensions.
As we saw in the beginning of this post, FeedForwardNetwork simply wraps haiku.transform’s pure functions (init and apply) into an Acme container.
Why rng key?
JAX shuttles around these explicit (pseudo-)random number generator parameters in the functions that require them. In this way, you can reproduce experiments without worrying that a different seed is causing you uncertainty in your results behind the scenes. All in the name of good science!
Why is this explicitness necessary? Normally, Python will, from an initial seed, maintain a global key which functions will then access, generating random numbers. This is fine and dandy if there is a single thread of execution. For example, consider the following code.
Python will always run randomSum() the same way, according to a well-defined operator precedence. funA() is called (first random number from seed 42), then 2*funB() is calculated, at which time funB() is called (second random number from seed 42), then they are summed. If funB ran before funA on occasion, the final output would change. This never happens. The output of randomSum() will always be the same, i.e. reproducible!
Feel free to add some print statements and run the code to satisfy any doubts.
If we are parallelizing our code (the whole point of using JAX!), we don’t know what order functions will be called in, due to how your OS handles process scheduling. funA() and funB() above to different processes, sometimes funB() might run first. As a result, using a global random key causes us to sacrifice our beloved reproducibility. Thus, we must explicitly give each process its own specific key, which it can then use in its own good time, regardless of execution order, in a reproducible, well-defined fashion.

So, we have our network defined and transformed. Recalling our container class:
All that remains is a little book-keeping to expose sample() and log_prob() functions. First, assume we have a way of getting at the policy’s output parameterizing a normal distribution, params (which, recall, is (mean_out, var_out)). With this we’ll be able sample() the policy. Now that we have the action returned from this sample(), we can also calculate the log_prob(). We just need to use some functions from the tensorflow_probability library. While we focus on continuous distributions in this post, the procedure is similar for categorical distributions.
Finally, just a bit more glue and book-keeping to take care of exposing an easy and organized way of getting our actions and associated log probabilities in one function call, inference(params, key, observations).
Whew! We made it past the first line! Surprisingly, most of the hard code is behind us, and we get to jump into the algorithm proper.

The RL loop
You should already have an understanding of the full loop before we proceed (see here).
Let’s dive into each component individually.
The third line

Collect set of trajectories
We’re going to start at the level of the training loop and drill our way down. We’re going to start seeing a fair bit of Acme machinery for creating and training our agents, but I’ll sweep most of the extraneous stuff under the rug.
Entering run_episode():
There’s quite a bit going on here. First the environment is initialized (reset), and we store the first observation in Reverb. Because VPG is an online algorithm, we don’t have a replay buffer; we’re simply storing enough transitions from our trajectory for the next learner step.
Through a series of RL/Acme boilerplate, we send our observation through the neural net representing the policy and sample an action from the output distribution. We step() the environment with this action, and store the transition/timestep in Reverb with observe(). Finally, in update(), if there are enough transitions to make up a full batch, the learner (contained within the actor object) will perform a training step (detailed in the following sections), and update the actor with the resultant new parameters.
The fourth line

Compute future returns.
The theory of this has been discussed in a previous post; with that in mind the following code block should be self-explanatory.
However, we wish to use generalized advantage estimation, so we take advantage of an rlax function to compute the advantages for us, vectorizing over the batch dimension with jax.vmap(). This takes place on a single device (GPU).
Lines 5 & 7a

Compute the policy gradient, and compute the value function gradient
The theory of the policy gradient has been discussed in a previous post, and we discuss using the advantages instead of the future return \(R_t\) here, and we describe the value function loss here.
With that in mind the following code block should be self-explanatory. We run inference on the observations to get our policy and value network outputs, and use this output combined with the advantages and target_values (\(R_t\)), to calculate the policy loss and value functions, respectively. Then we run jax.grad(), and voila, we have the gradient to update our networks with! Very simple. The function also takes care of normalization of input advantages.
As a reminder, here’s the policy gradient:
\[\hat{g}=\frac{1}{\left| \mathcal{D}_k \right|}\sum_{\tau\in \mathcal{D}_k}\sum_{t=0}^{T}\nabla _{\theta}\log\pi_\theta (a_t\vert s_t)_{\theta _k} A_t\]And here’s the value loss, used to compute the value gradient:
\[\frac{1}{\left\vert \mathcal{D}_k \right\vert T}\sum_{\tau\in \mathcal{D}_k}\sum_{t=0}^{T}\left(V_\phi(s_t)-\hat{R}_t \right)^2\]Lines 6 & 7b

Update the policy and value functions with their respective gradients.
This part should be familiar to anyone with a passing interest in deep learning. With our optimizer (e.g., Adam), we update the model parameters with our computed gradients.
Putting it together
The remainder of the code is relatively boilerplate as far as reinforcement learning goes. In short, sgd_step() is run over the batch (collected trajectories $\mathcal{D}_k$) in a loop of minibatches with jax.lax.scan(). This happens on each device (GPU), by broadcasting to all available devices with jax.pmap(). It’s really as simple as it sounds, once you understand the syntax!
The outer RL loop then starts again, collecting trajectories $\tau$ with the actor, which may update its policy from the learner, which acts as a network parameter server to all running actors. Trajectories are stored with DeepMind’s Reverb, and accessed by the learner each learner step by accessing Reverb through a Python iterator interface. You can think of Reverb as a fancy FIFO implemented as a table.
For more information about this information flow, and also how it is easily extended to multiple actors and learners, potentially across multiple machines, check out DeepMind’s Acme library on GitHub.
Performance and improvements
Unfortunately, VPG does not perform very well at all. There are reasonable additions and improvements which weren’t discussed in this post which are typically added to any reinforcement learning algorithm to improve its robustness, mainly boiling down to normalization of inputs to the loss functions used for calculating gradients. You’ll see these have been added to the code. And yet, even on a simple environment like gym:Pendulum-v1, we see practically no learning. Check out these benchmarks from OpenAI; VPG’s performance is pitiful compared to modern algorithms.
So this begs the question… why on earth did we go through all these pesky details if it was all for nothing?
VPG is a stepping stone!
It was not a waste; we’ll see why. Recall all we’ve learned up to this point: we’ve…
- Understood policies: acting from state
- Collected trajectories with said policies
- Understood future return, value functions, and advantage estimation
- Understood how to define networks in JAX/haiku
- Understood how to take loss gradients in JAX and apply gradient updates
- Learned the policy and value function in an RL loop
Let’s take our VPG code which uses all of the concepts we’ve discussed, and make one single change.
The line which computes the policy loss (the policy gradient without the grad) looks like this:
Let’s just swap this out with
where the behavior_log_probs are the same term as policy_log_probs, only they were calculated earlier, with an older version of the policy network. Let’s skip the details of the rlax.clipped_surrogate_pg_loss() function.
With this simple change, we go from no performance to great performance on Pendulum-v1.
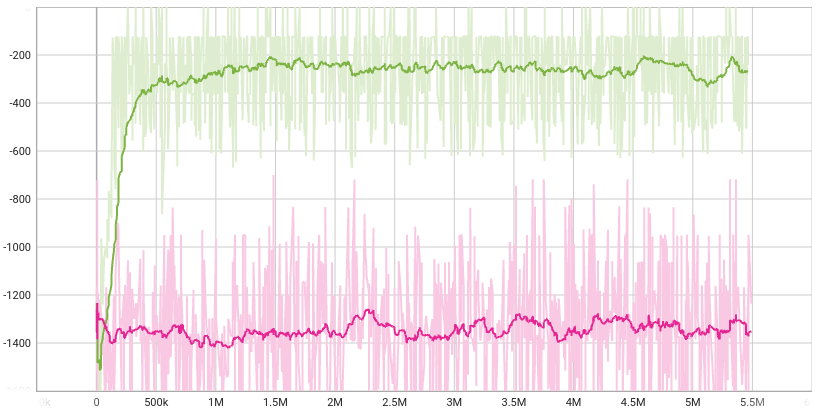
…a stepping stone to PPO
Wow! How on earth did this happen? Well, this isn’t VPG anymore, it’s PPO, or Proximal Policy Optimization, a ubiquitous and effective algorithm which many practitioners use as a baseline for all other algorithms. (Also, it does take a few more lines to calculate behavior_log_probs.) There are many, many resources from which to learn PPO, which I’ll leave you to find on your own.
Suffice it to say that by swapping out our policy loss term with a “surrogate loss” which doesn’t allow for too-large policy updates, we can stabilize training and be off to the races. The important takeaway here is that you are now 90% of the way to understanding all policy gradient algorithms, and you’re not doing too bad with all actor-critic algorithms either. Things do get a little more subtle from here on, but you have the foundation. Pat yourself on the back!
I recommend you take a look to see the rest of the code that pieces this together here. As this has merely been modified from the Acme PPO implementation, the obvious next step would be to take a look at that and other resources explaining PPO, and perhaps the rlax surrogate loss function above. As your path continues, you’ll find that even PPO has a lot of room for improvement. Good luck!
Thank you for reading, and come again soon!