Continuous Log Likelihood
A quick and dirty derivation
Strangely, I couldn’t find anyone else who had done the math for the log likelihoods of multivariate normal distributions online. Let’s be good scientists and double check anything that isn’t obvious, especially if it’s widely accepted.
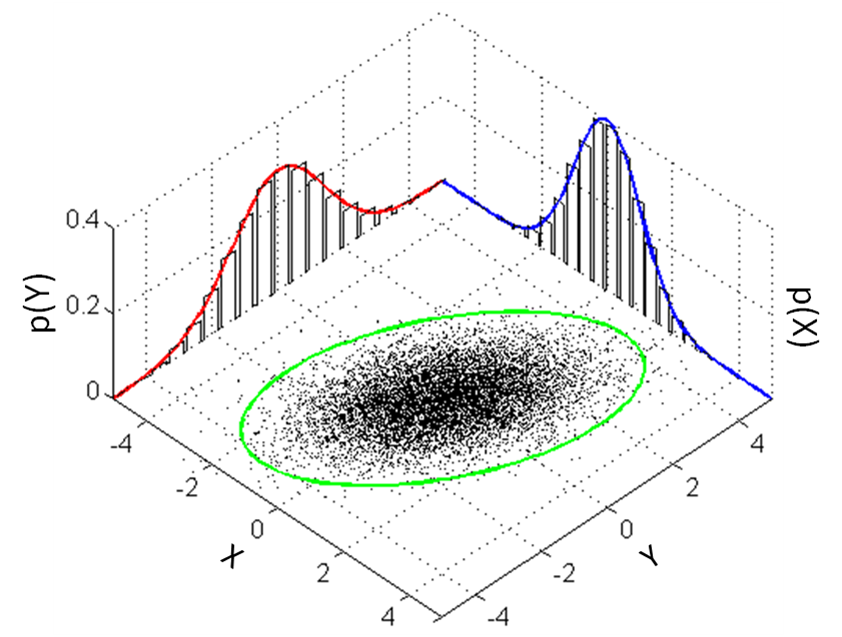
PDF of a multivariate normal distribution:
\[f(x) = \frac{1}{\left(2\pi\right)^{\frac{k}{2}}\left| \Sigma \right|^{\frac{1}{2}}}\exp\left(-\frac{1}{2}\left(x-\mu\right)^T\Sigma^{-1}\left(x-\mu\right)\right)\]where \(\Sigma\) is the (diagonal) covariance matrix, and \(\mu\) is the column vector of means for each dimension. \(x\) is the column vector of positions along the probability density function whose likelihoods we’re interested in.
Take the log of both sides:
\[\log \left(f(x)\right) = \log \left(\frac{1}{\left(2\pi\right)^{\frac{k}{2}}\left| \Sigma \right|^{\frac{1}{2}}}\exp\left(-\frac{1}{2}\left(x-\mu\right)^T\Sigma^{-1}\left(x-\mu\right)\right)\right)\]Annihilate the exponent and use a log identity to add the multiplied terms:
\[= \log \left(\frac{1}{\left(2\pi\right)^{\frac{k}{2}}\left| \Sigma \right|^{\frac{1}{2}}}\right) -\frac{1}{2}\left(x-\mu\right)^T\Sigma^{-1}\left(x-\mu\right)\]Let’s look at the left term first:
\[\log \left(\frac{1}{\left(2\pi\right)^{\frac{k}{2}}\left| \Sigma \right|^{\frac{1}{2}}}\right)\]Use some log identities:
\[=-\frac{k}{2}\log 2\pi - \log \left|\Sigma \right|^{\frac{1}{2}}\]The determinant of a diagonal matrix is the product of its diagonal elements:
\[=-\frac{k}{2}\log 2\pi - \log \prod_{i=1}^{k}\Sigma_{i,i}^{\frac{1}{2}}\]The log of a product of terms is the sum of the logs of those terms (and applying the element-wise square root, and some rearranging):
\[=-\frac{1}{2}\left(k\log 2\pi + \sum_{i=1}^{k}2\log\sigma_{i}\right)\]Halfway done. Now let’s look at the right term of the main equation:
\[-\frac{1}{2}\left(x-\mu\right)^T\Sigma^{-1}\left(x-\mu\right)\]Ok, time to break out the linear algebra. Notice here \(n\) stands for the number of dimensions (in our RL application, the dimensionality of the continuous action space).
\[=-\frac{1}{2}\begin{bmatrix} x_1-\mu_1, & x_2-\mu_2, & \dots, & x_n-\mu_n\end{bmatrix} \; \begin{bmatrix} 1/\sigma^2_1 & & &\\& 1/\sigma^2_2 &&\\ &&\ddots &\\ &&&1/\sigma^2_n \end{bmatrix} \; \begin{bmatrix} x_1-\mu_1 \\ x_2-\mu_2 \\ \vdots \\ x_n-\mu_n\end{bmatrix} \;\] \[=-\frac{1}{2}\begin{bmatrix} (x_1-\mu_1)/\sigma^2_1 & (x_2-\mu_2)/\sigma^2_2 & \dots & (x_n-\mu_n)/\sigma^2_n\end{bmatrix} \; \begin{bmatrix} x_1-\mu_1 \\ x_2-\mu_2 \\ \vdots \\ x_n-\mu_n\end{bmatrix} \;\] \[=-\frac{1}{2}\sum_{i=1}^k\frac{(x_i-\mu_i)^2}{\sigma_i^2}\]Adding the first and second terms gives the result:
\[\log \left(f(x)\right)=-\frac{1}{2}\left(k\log 2\pi+\sum_{i=1}^k\left[\frac{(x_i-\mu_i)^2}{\sigma_i^2}+2\log\sigma_i\right]\right)\]I recommend going through it yourself! After all:
What I cannot create, I do not understand.
-Richard Feynman
And one more for the road:
In mathematics you don’t understand things.
You just get used to them.
-John Von Neumann